R Markdown - A Better Way of Communicating with Data
Danyang Dai
The University of Melbourne
August 24, 2020
https://rmarkdown-rladiesmelbourne.netlify.app
About Me
- Graduated from Monash University with Bachelors of Commerce in 2018
- Currently a Masters Student at the University of Melbourne
Why R Markdown
Why R Markdown
Why R Markdown

Hypothesis testing
Why R Markdown

Hypothesis testing
Bayesian Estimation and Graphical presentation
Why R Markdown

Hypothesis testing
Bayesian Estimation and Graphical presentation
Demonstration of Reproducible report
Case Study - Hypothesis Testing
Example - yearly wage of 474 bank employees
- y: natural logarithm of salary (LOGSAL)
- x1: individual's number of completed years of schooling (EDUC)
- x2: information on the employee's gender (GENDER: 0 for females, 1 for males)
- x3: whether or not they belong to a minority group (MINORITY : 0 for non-minority, 1 for minorities)
- x4: a categorical variable indicating the nature of the position in which the individual is employed (JOBCAT: 1 for administrative jobs, 2 for custodial jobs, and 3 for management jobs)
- We are interested in testing hypotheses in the model
- y=β0+βeducx1+βgenderx2+βminorityx3+βjobcatx4+ui
Data provided by Professor Chris Skeels in Econometrics 3 ECOM90013
Hypothesis Testing
Does Education affect annual salary?
H0:βeduc=0
H1:βeduc≠0
## LM Testlm0 <- lm(LOGSAL ~ GENDER + MINORITY + JOBCAT, data = wages)e0 <- residuals(lm0)lm1 <- lm(e0 ~ EDUC + GENDER + MINORITY + JOBCAT, data = wages)e1 <- summary(lm1)e1rsq <- e1$r.squaredtest1 <- nrow(wages) * e1rsq```{r, echo = FALSE, result = 'asis'}cat( "Under the null hypothesis with degree of freedom equal to 1,", " the test statistic is ",round(test1,4), " and critical value is ", round(qchisq(0.95,1),4))```Under the null hypothesis with degree of freedom equal to 1 , the test statistic is 125.7683 and the critical value is 3.8415.
Does Education affect annual salary?
H0:βeduc=0
H1:βeduc≠0
reject_h0 <- test1 > round(qchisq(0.95, 1), 4)Since the test statistic for LM1 is `r if(reject_h0) "greater" else "smaller" ` greater than the critical, therefore we `r if(reject_h0) "" else " cannot" ` reject the null hypothesis and conclude that βeduc is `r if(reject_h0) "" else " not"` significant at 5% level.
Since the test statistic for LM1 is greater than the critical, therefore we reject the null hypothesis and conclude that βeduc is significant at 5% level.
Easy? Let's do another one!
Does Minority and Job category affect salary?
H0:βminority=
βjobcat=0
H1:βminority≠0
or βjobcat≠0
lmrest <- lm(formula = LOGSAL ~ EDUC + GENDER, data = wages)e2 <- summary(lmrest)$residualslme2 <- lm(e2 ~ EDUC + GENDER + MINORITY + JOBCAT, data = wages)e2.sqr <- summary(lme2)$r.squaredtest2 <- nrow(wages) * e2.sqrprint("Under the null hypothesis with degree of freedom equal to 2")## [1] "Under the null hypothesis with degree of freedom equal to 2"print(paste0("the test statistic is ", round(test2, 4)))## [1] "the test statistic is 208.745"print(paste0("The critical value is ", round(qchisq(0.95, 2), 4)))## [1] "The critical value is 5.9915"Does Minority and Job category affect salary?
H0:βminority=
βjobcat=0
H1:βminority≠0
or βjobcat≠0
reject_h0.2 <- test2 > round(qchisq(0.95, 2), 4)Since the test statistic for LM1 is
`r if(reject_h0.2) "greater" else "smaller"`greater than the critical, therefore we`r if(reject_h0.2) "" else " cannot" `reject the null hypothesis and conclude that`r if(reject_h0.2) "at least one of" else "none of" `at least one of βminority and βjobcat is significant at 5% level.Since the test statistic for LM1 is greater than the critical, therefore we reject the null hypothesis and conclude that at least one of βminority and βjobcat is significant at 5% level.

Bayesian Approach - Prior Adjustments
Bayes' Rule: p(θ|Y)∝L(θ|Y)p(θ)
The posterior distribution is proportion to the kernel of posterior distribution times the distribution of the prior distribution.
Bayesian Approach - Prior Adjustments
Bayes' Rule: p(θ|Y)∝L(θ|Y)p(θ)
The posterior distribution is proportion to the kernel of posterior distribution times the distribution of the prior distribution.
We have a time series for Australian real GDP from the Australian Real-Time Macroeconomic Database containing T=230 observations on the quarterly data from quarter 3 of 1959 to the last quarter of 2016.
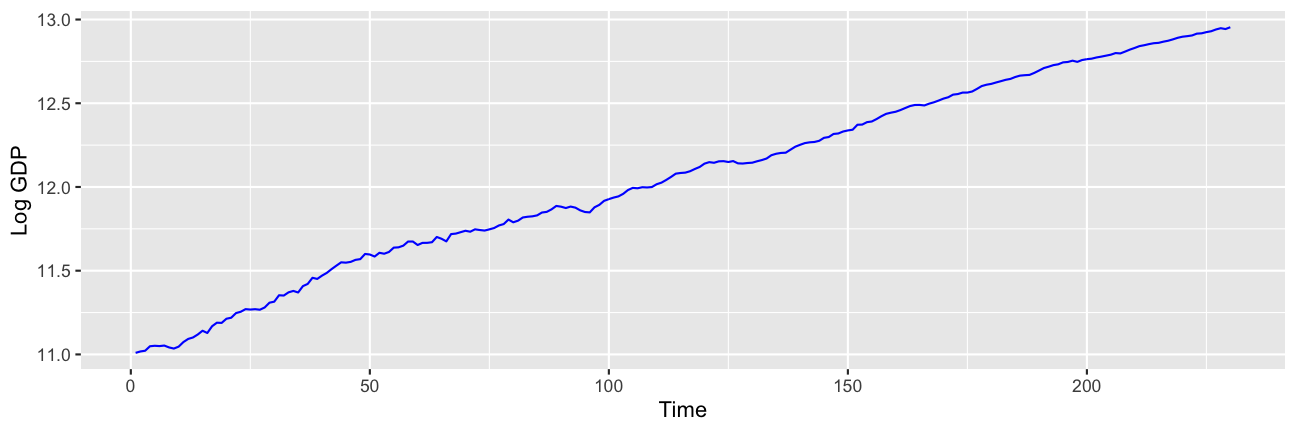 Data provided by Tomasz Wozniak in Macroeconometrics ECOM90007
Data provided by Tomasz Wozniak in Macroeconometrics ECOM90007
Setting Prior distributions parameters
Question: "Set the parameters of the natural-conjugate prior distribution and motivate the values that you choose."
Random Walk with drift process: logGDPt=μ0+αlogGDPt−1+ut
α=1
ut∼N(0,σ2)
P(σ2)∼IG2(s,ν)
Priors: μ0, α, σ2, s, ν
Setting Prior distributions parameters
Question: "Set the parameters of the natural-conjugate prior distribution and motivate the values that you choose."
Random Walk with drift process: logGDPt=μ0+αlogGDPt−1+ut
α=1
ut∼N(0,σ2)
P(σ2)∼IG2(s,ν)
Priors: μ0, α, σ2, s, ν

First set of priors testing
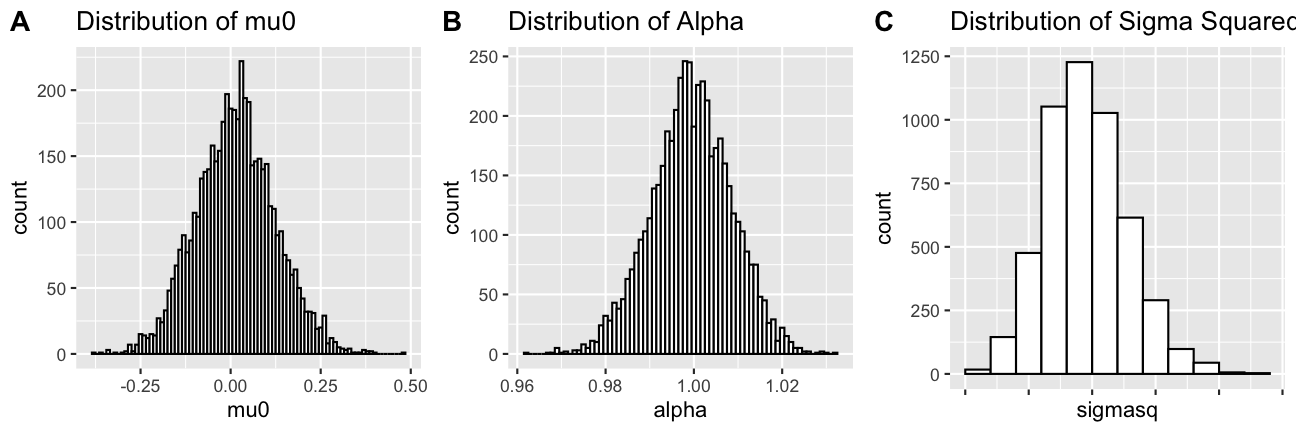
- P(β=[μ0α]|σ2)∼N([0.011],σ2[10010])
The sample mean of μ0 with 5000 draws is 0.0148564 and the variance is 0.011913.
The sample mean of α with 5000 draws is 0.999454 and the variance is 0.000082.
The sample mean of σ2 with 5000 draws is 0.017256 and the variance is 0.0000026.
Adjust prior parameters
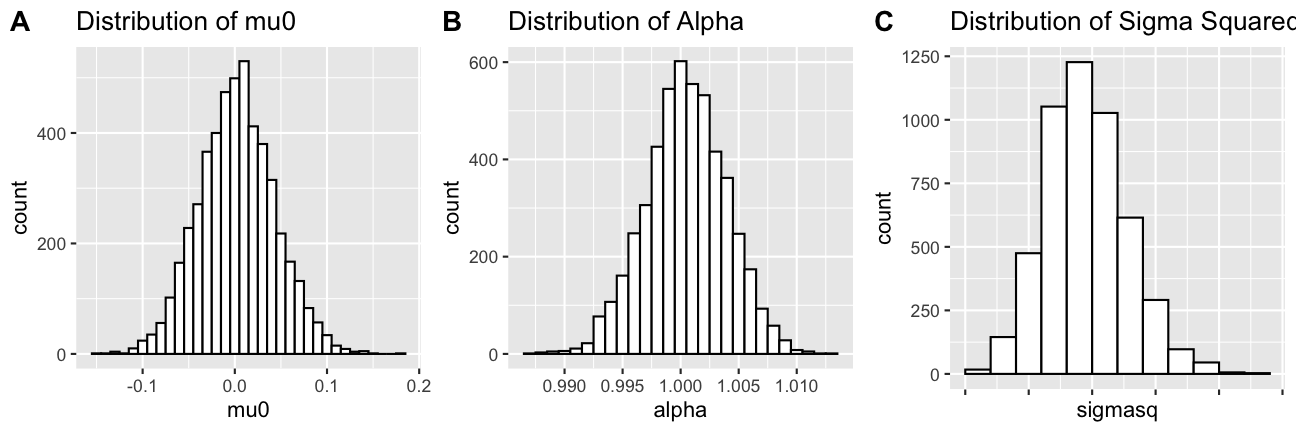
- P(β=[μ0α]|σ2)∼N([0.011],σ2[0.1001])
The sample mean of μ0 with 5000 draws is 0.0024582 and the variance is 0.001686.
The sample mean of α with 5000 draws is 1.00048 and the variance is 0.000012.
The sample mean of σ2 with 5000 draws is 0.017258 and the variance is 0.0000026.
Adjust prior parameters
- P(β=[μ0α]|σ2)∼N([01],σ2[1001])
The sample mean of μ0 with 5000 draws is 0.0114882 and the variance is 0.011913.
The sample mean of α with 5000 draws is 0.999733 and the variance is 0.000082.
The sample mean of σ2 with 5000 draws is 0.017257 and the variance is 0.0000026.
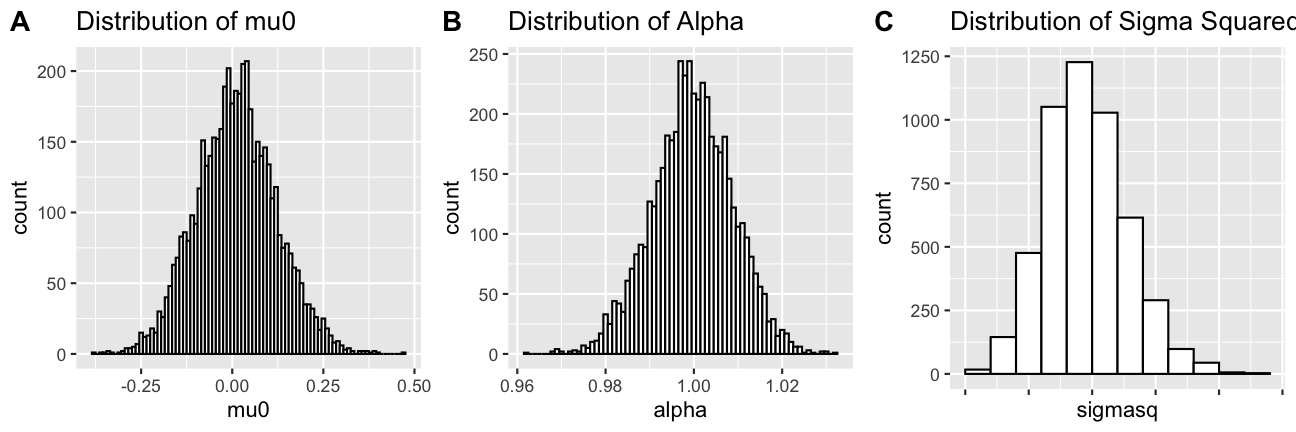
Behind the Scenes
The sample mean of μ0 with 5000 draws is
`r round(mean(blogau$V1),8)`and the variance is`r round(var(blogau$V1),6)`.The sample mean of α with 5000 draws is
`r round(mean(blogau$V2),6)`and the variance is`r round(var(blogau$V2),8)`.The sample mean of σ2 with 5000 draws is
`r round(mean(blogau$sigmasq),6)`and the variance is`r round(var(blogau$sigmasq),8)`.
shh, witchcraft here. Why do I need this chunk to advance to next slide?@yihui, please send help!Outputting Plots
R Script
pdf(file="mu0plot.pdf", height=12, width=9)ggplot(data=blogau, aes(x=V1)) + geom_histogram(binwidth=0.01, colour="black", fill="white")+ ggtitle("Distribution of mu0")+ xlab("mu0") dev.off()Outputting Plots
R Script
pdf(file="mu0plot.pdf", height=12, width=9)ggplot(data=blogau, aes(x=V1)) + geom_histogram(binwidth=0.01, colour="black", fill="white")+ ggtitle("Distribution of mu0")+ xlab("mu0") dev.off()R Markdown
```{r,echo=FALSE,fig.height=12,fig.width=9,dev="pdf"}ggplot(data=blogau, aes(x=V1)) + geom_histogram(binwidth=0.01, colour="black", fill="white")+ ggtitle("Distribution of mu0")+ xlab("mu0") ```Reference
Alison Hill, June 2019, R-Ladies xaringan theme:
Professor Chris Skeels, S1 2020,Econometrics ECOM90013, University of Melbourne
Guidotti, E., Ardia, D., (2020), "COVID-19 Data Hub", Journal of Open Source Software 5(51):2376, doi:10.21105/joss.02376.
Tomasz Wozniak, S1 2020, Macroeconometrics ECOM90007, University of Melbourne
Sources
R Markdown: The Definitive Guide
Workshops: Communicating with Data via R Markdown by Emi Tanaka
Recent Talks about R Markdown on the 2020 RStudio Conference:
One R Markdown Document, Fourteen Demos by Yihui Xie
How Rmarkdown changed my life by Professor Rob J Hyndman
Questions?

Stay in Touch

danyangd@student.unimelb.edu.au
https://www.linkedin.com/in/danyang-dai-7529b4152/